12th भौतिकी अध्याय 1 विद्युतीय आवेश एवं क्षेत्र लघु प्रश्नउत्तर

प्रिय छात्रों कक्षा 12 के अध्याय 1 वैद्युत आवेश एवं क्षेत्र महत्वपूर्ण लघु उत्तरीय प्रश्न उत्तर के साथ एक स्थान पर एकत्र किए गए हैं ताकि आप सभी को अपनी 12 बिहार बोर्ड परीक्षा के साथ-साथ यूपी बोर्ड परीक्षा, झारखंड बोर्ड परीक्षा, एमपी बोर्ड परीक्षा ,राजस्थान बोर्ड परीक्षा, और अन्य बोर्ड परीक्षाओं के लिए तैयार किया जा सके। अधिक सहायता के लिए मेरे नवेंदु क्लासेस यूट्यूब चैनल पर जाएं।

Read In English

प्रश्न(1) - विद्युत्आवेश के दो मूल गुणों को लिखे।

बिहार बोर्ड- 2012
उतर:-आवेश के दो गुण निम्न है।
(i) आवेश क्वाण्टमीकृत होता है।

(ii) आवेश संरक्षित होता है।

प्रश्न (2)- आवेश संरक्षण का सिद्धांत क्या है ?

बिहार बोर्ड- 2020 ,2022 उत्तर- "किसी विलगित निकाय का कुल आवेश स्थिर रहता है"। इसे आवेश संरक्षण का सिद्धांत कहते है। ${{e}^{-}}+{{e}^{+}}=\gamma +\gamma $ कुल आवेश =0 कुल आवेश =0

प्रश्न(3) - क्या फोटॉन पर आवेश संभव है ?

उतर:- फोटॉन ऊर्जा का एक पैकेट है | जिसके ऊर्जा का मान “h$\nu $” होता है जहां h = प्लान्क स्थिरांक तथा $\nu $=विकिरण कीआवृत्ति|चुँकि हम जानते है की फोटॉन का विराम द्रव्मान (rest mass) शुन्य होता है | अतः इस पर कोई आवेश नहीं रह सकता |

प्रश्न(4) -क्या किसी वस्तु को आवेशित करने पर उसका द्रव्यमान बदल जाएगा ?

उतर:- किसी वस्तु का आवेशित होना इलेक्ट्रान के आदान - प्रदान पर निर्भर करता है | यदि कोई वस्तु को ऋणावेशित होती है तो इलेक्ट्रान का ग्रहण करती है जिससे द्रव्यमान बढ़ जाता है तथा जब कोई वस्तु धनावेशित होतीं है तो इलेक्ट्रान त्याग करती है | जिससे उसका द्रव्यमान घट जाता है |

प्रश्न(5)- कूलाम बल को सदिश रूप में लिखने से क्या लाभ है ?

उतर - कूलाम बल को सदिश रूप में लिखने से निम्नलिखित लाभ है |

(i)सदिश रूप में लिखने से पता चलता है की दो आवेशो द्वारा एक दुसरे पर लगा कूलाम बल परिमाण में बराबर तथा दिशा में एक दुसरे के विपरीत होते है |

(ii ) सदिश रूप में लिखने से यह पता चलता है की कूलाम बल दोनों आवेशो के मिलाने वाली रेखा के अनुदिश लगता है | अर्थात कूलाम बल एक केन्द्रीय बल है |

अध्याय 1

प्रश्न(6)- कूलाम बल को केन्द्रीय बल कहते है क्यों ?

उतर -

कूलाम बल दोनों आवेशो के मिलनेवाली रेखा के अनुदिश लगता है ,यही कारण है की कूलाम बल को केन्द्रीय बल कहते है |

प्रश्न(7) -कूलाम बल की सीमाए क्या क्या है ?

उतर - कूलाम बल की निम्नलिखित सीमाए है |

(i)यह बल केवल बिंदु आवेशो के बीच लगता है |

(ii)यह बल स्थिर आवेशो लिए लागू होता है |

(iii)यदि आवेश किसी स्वेच्छित (मनमाने )आकार में हैं तो इसे लागू करना मुश्किल है क्योंकि उन स्थितियों में हम आवेशों के बीच की दूरी निर्धारित नहीं कर पाते हैं।

प्रश्न(8) -विद्युतीय क्षेत्र की तीव्रता से आप क्या समझते हैं ? बिहार बोर्ड- 2020 उत्तर- विद्युत क्षेत्र- इकाई धनात्मक (परीक्षण) आवेश पर लगने वाले बल को विद्युतीय क्षेत्र की तीव्रता कहते हैं। विद्युतीय क्षेत्र की तीव्रता = बल / आवेश \[E=\frac{F}{q}\] प्रश्न(9)-धारावाही चालक में विद्युतीय क्षेत्र की तीव्रता तथा समविभवी तल को परिभाषित कीजिए।

बिहार बोर्ड- 2013 उत्तर- विद्युतीय क्षेत्र की तीव्रता- इकाई धनात्मक (परीक्षण) आवेश (धारावाही चालक के किसी भी बिंदु पर) पर लगने वाले बल को विद्युतीय क्षेत्र की तीव्रता कहते है।

विद्युतीय क्षेत्र की तीव्रता = बल / आवेश \[E=\frac{F}{q}\] समविभवी तल - वह पृष्ठ जिसके सभी बिंदुओं पर विभव समान हो, उसे समविभवी तल कहते है।

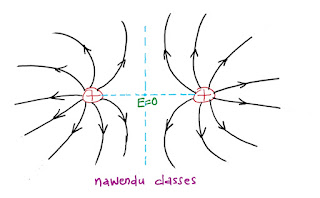
विद्युत क्षेत्र हमेशा एक समविभवी तल के लंबवत होता है। प्रश्न (10) -दो समान बिंदु आवेशों के निकाय के कारण विद्युत क्षेत्र के बल की रेखाएँ खींचिए। बिहार बोर्ड- 2017

उत्तर-

या

दो समान बिंदु आवेशों के निकाय के कारण विद्युत क्षेत्र के बल की रेखाएँ खींचिए।

प्रश्न (11) -विधुतीय बल रेखाओ और चुम्बकीय बल रेखाओ मे अंतर स्पष्ट करें |

उतर:-विधुतीय बल रेखायें चुम्बकीय बल रेखायें
(¡)विधुतीय बल रेखाएँ लूप नहीं बनाती है | (¡)चुम्बकीय बल रेखाएँ लूपबनाती है |

(¡¡)विधुतीय बल रेखाएँ चालक के तल के (¡¡)चुम्बकीय बल रेखाएँ चालक के तल से

लम्बवत निकलती है | किसी भी कोण पर निकलती है |

(¡¡¡)विधुतीय बल रेखाएँ चालक के भीतर (¡¡¡)चुम्बकीय बल रेखाएँ चालक के भीतर

नही होती है | होती है |

प्रश्न(12)- विधुतीय बल रेखाओ एक- दुसरे को नहीं कटती है क्यों? क्या दो समविभव पृष्ठ प्रतिच्छेद कर सकते हैं?

बिहार बोर्ड- 2014

उतर:-

विद्युतीय बल रेखाए एक दुसरे को नहीं कटती है। क्योकि ऐसा होने पर एक ही बिंदु पर विद्युतीय क्षेत्र कि दो दिशाए होंगी, जो संभव नहीं है।

विद्युतीय क्षेत्र की दिशा समविभवी तल के लंबवत होती है। यदि दो समविभव पृष्ठ एक-दूसरे को प्रतिच्छेद करते हैं तो उनके पास प्रतिच्छेदन के प्रत्येक बिंदु पर विद्युत क्षेत्र की दो भिन्न दिशाएँ होंगी जो संभव नहीं है , इसलिए दो समविभव पृष्ठ कभी भी एक-दूसरे को प्रतिच्छेद नहीं करते हैं।

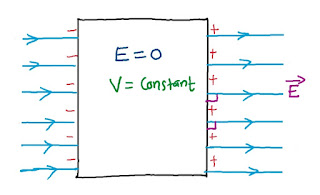
प्रश्न (13)-विधुतीय क्षेत्र में किसी चालक को रखने पर वह कैसा व्यवहार करेगा ?

उतर:-

(¡)सामने वाले पृष्ट पर ऋणआवेश तथा विपरीत पृष्ट पर धनावेश उत्पन्न हो जाएगा |

(¡¡)विधुतीय क्षेत्र चालक के तल पर लम्बवत होगा |

(¡¡¡)चालक के भितर विधुतीय क्षेत्र शुन्य होगा |

(¡v)आवेश केवल बाहरी सतह पर होगा |

(v)चालक के सतह पर एवं उसके भीतर विधुतीय विभव नियत होता है |

प्रश्न(14)- स्थिरवैद्युत परिरक्षण क्या है? इसका कोई एक व्यावहारिक अनुप्रयोग बताइये । बिहार बोर्ड- 2014 उत्तर- स्थिरवैद्युत परिरक्षण - किसी वस्तु या व्यक्ति को खोखले चालक के अंदर रखकर विद्युतीय क्षेत्र (या विद्युत् धारा ) से परिरक्षित करने की घटना को स्थिरवैद्युत परिरक्षण कहते है। यह घटना इस तथ्य पर आधारित है कि एक (खोखले) चालक के अंदर विद्युत क्षेत्र शून्य है, अनुप्रयोग - आकाशीय बिजली से बचने के लिए कार के अंदर बैठना सुरक्षित होता है।

प्रश्न(15) - विधुत मशीनों में तीखा नोंक नहीं छोड़ा जाता है , क्यों ?

उतर:- तीखे नोंक का पृष्ट क्षेत्रफल बहुत कम होता है जिसके कारण उसका पृष्ट आवेश घनत्व ($\sigma =\frac{Q}{A}$) बहुत अधिक होता है | पृष्ट आवेश घनत्व बहुत अधिक होने के कारण तीखे नोंक की तीव्रता का ($E=\frac{\sigma }{\mathop{\varepsilon }_{o}}$ )मान बहुत अधिक हो जाएगा | जिसके कारण तीखा नोक से कोरोना डिस्चार्ज होने लगेगा | यहीं कारण है की विधुत मशीनों से तीखा नोंक नहीं छोड़ा जाता है।

प्रश्न(16)- परावैद्युत शक्ति और आपेक्षिक विद्युतशीलता को परिभाषित करें। बिहार बोर्ड- 2010 ,16 उत्तर - परावैद्युत शक्ति - किसी परावैद्युत माध्यम के लिए विद्युत क्षेत्र का वह मान जिसके बाद वह कुचालक से सुचालक बन जाता है (अर्थात अपने कुचालक गुण को खो देता है) परावैद्युत शक्ति कहलाता है। *हवा की परावैद्युत शक्ति \[6\times {{10}^{6}}\]V/m है। आपेक्षिक विद्युतशीलता (या परावैद्युत स्थिरांक) - किसी माध्यम की विद्युतशीलता और हवा या निर्वात की विद्युतशीलता के अनुपात को आपेक्षिक विद्युतशीलता कहते है।

आपेक्षिक विद्युतशीलता = किसी माध्यम की विद्युतशीलता /हवा या निर्वात की विद्युतशीलता ${{\varepsilon }_{r}}=\frac{\varepsilon }{{{\varepsilon }_{0}}}$

प्रश्न(17) -क्या 1m त्रिज्या के गोले को 1C आवेश दिया जा सकता है ?

उत्तर:- यदि r त्रिज्या के गोले पर Q आवेश दिया जाए तो सतह पर विद्युतीय क्षेत्र

E = Q/4π${{\varepsilon }_{o}}$$\times $r²

यदि Q= 1 C

r=1 m , तो

E = 1/4π${{\varepsilon }_{o}}$$\times $ 1

E = 9×10⁹v/m
यह विद्युतीय क्षेत्र हवा के परावैद्युत शक्ति से अधित है | अतः 1m त्रिज्या के गोलिय चालक पर 1c आवेश नहीं दिया जा सकता है |

प्रश्न(18)- निर्वात की विद्युतशीलता का मात्रक और विमा लिखिए। बिहार बोर्ड- 2018 उत्तर- मात्रक - \[F=\frac{1}{4\pi {{\varepsilon }_{0}}}\times \frac{{{q}_{1}}{{q}_{2}}}{{ {r}^{2}}}\] ${{\varepsilon }_{0}}=\frac{{{q}_{1}}{{q}_{2}}}{4\pi F{{r}^{2}}}= \frac{C\times C}{N\times {{m}^{2}}}={{C}^{2}}{{N}^{-1}}{{m}^{-2 }}$ तो, (निर्वात के) विद्युतशीलता का एस.आई. मात्रक ${{C}^{2}}{{N}^{-1}}{{m}^{-2}}$ होता है।

विमा - ${{\varepsilon }_{0}}=\frac{{{q}_{1}}{{q}_{2}}}{4\pi F{{r}^{2}}}= \frac{AT\times AT}{ML{{T}^{-2}}\times {{L}^{2}}}={{M}^{-1}}{{L}^{- 3}}{{T}^{4}}{{A}^{2}}$ तो, (निर्वात के) विद्युतशीलता की विमा ${{M}^{-1}}{{L}^{-3}}{{T}^{4}}{{A}^{2}}$ होता है। प्रश्न (19) - विद्युतीय फ्लक्स को परिभाषित करें तथा इसका S.I मात्रक लिखिए। बिहार बोर्ड- 2019 उत्तर - विद्युतीय फ्लक्स- विद्युतीय क्षेत्र और क्षेत्रफल सदिश के बिंदु गुणनफल को विद्युतीय फ्लक्स कहते है। विद्युतीय फ्लक्स = $\varphi =\vec{E}.\vec{A}$ एस.आई. इकाई- $\varphi =E\times A=\frac{V}{m}\times {{m}^{2}}=Vm$ या $\varphi =E\times A=\frac{N}{C}\times {{m}^{2}}=N{{m}^{2}}/C$ विद्युतीय फ्लक्स का एस.आई. मात्रक Vm या $N{{m}^{2}}/C$ होता है।

प्रश्न(20)- साधारण रबड़ विधुत का कुचालक होता है लेकिन वायुयान के पहिया में प्रयुक्त होने वाले रबर हल्के सुचालक बनाए जाते है , क्यों ?

उतर - साधारण रबड़ विधुत का कुचालक होता है लेकिन वायुयान के पहिए में प्रयुक्त होने वाले रबड़ हल्के सुचालक बनाएं जाते है ताकि वायुयान धरती (पृथ्वी ) के संपर्क में आते समय पहिए और ट्रेक के घर्षण के कारण पहिए पर उतपन्न अत्यधिक आवेश भूमिगत हो जाए और वायुयान किसी भी तरह के दुर्घटना से बचजाये। |

प्रश्न(21) - अत्याधिक ज्वलनशील पदार्थ को ढ़ोंनेवाले वाहनों से जमीन से छूती हुई धातु की चेन लटकती रहती है , क्यों ?

उतर - अत्याधिक ज्वलनशील पदार्थो को देने वाले वाहनों से जमीन को छूती हुई धातु की चेन इसलिए लटकी रहती है ताकि हवा और वाहनके घर्षण से उत्पन आवेश तथा पहिए और सड़क के घर्षण से उत्पन आवेश भुमिगत हो जाए और वाहन किसी भी तरह के दुर्घटना से वाहन बच जाए |

प्रश्न(22)-उच्च विभावन्तर के विधुत तारो से धारा प्रवाहित करने पर उस पर बैठी हुई चिड़िया उड़ जाती क्यों ?

उतर - उच्च विभंवातर के विधुत तारो से जब विधुत धारा प्रवाहित होती है तो उसपर बैठी हुई चिड़िया के दोनों पंखो पर प्रेरण के कारण समान आवेश पैदा होता है ,इन समान आवेशो में प्रतिकर्षण बल लगता है, जिसके कारण चिड़िया के दोनों पंख फैल जाते है और बैठी हुई चिड़िया उड़ जाती है |

प्रश्न(23) -वर्षा के समय धातु की मुठ वाली छातो की अपेक्षा बास की मुठ वाली छातो का उपयोग करना चाहिए क्यों ?

उतर - वर्षा के समय तड़ित की घटना होने पर विधुत का चालन धातु की छड़ से होकर हमारे शरीर से हो सकता हैं,जो हमारे लिए जान लेवा भी हो सकता हैं | इसी कारण बरसात के दिनों में होने वाले तड़ीत से अपने को सुरक्षित रखने के लिए बाँस के मुठ वाले छातें का उपयोग अच्छा होता है |

प्रश्न (24)- किसी खोखले चालक पर Q आवेश दिया गया है दिखाए की यह चालक के बाहरी तल पर स्थित होगा ?

उतर - खोखले चालक पर +Q आवेश दिया गया है | माना की ABC चालक के भीतर

बंद गाँसियन तल है |

गॉस के सिद्धांत के अनुसार ,

\[\oint{d\varphi =Q\times \frac{1}{{{\varepsilon }_{0}}}}\]

जहाँ Q = तल के भीतर का कुल आवेश

\[\oint{\vec{E}.d\vec{A}=Q\times \frac{1}{{{\varepsilon }_{0}}}}\]

\[\oint{EdA\cos {{0}^{^{{}^\circ }}}=\frac{Q}{{{\varepsilon }_{0}}}}\]

\[E\oint{dA}=\frac{Q}{{{\varepsilon }_{0}}}\]

लेकिन, हम जानते है की चालक के भीतर का विधुतीय क्षेत्र = E=0

अतः

Q=0

अर्थात खोखले चालक के भीतर में आवेश नहीं रहता है | अतः दिया गया आवेश खोखले चालक के तल पर वितरीत हो जाता हैं |

प्रश्न(25)- विद्युत क्षेत्रों के लिए अध्यारोपण का सिद्धांत बताएं और समझाएं।

                 बिहार बोर्ड- 2010 

 उत्तर-  अनेक आवेशों के कारण किसी बिंदु पर विद्युत क्षेत्र इन आवेशों द्वारा अलग-अलग उत्पन्न विद्युत क्षेत्रों के सदिश योग के बराबर होता है।

            $\vec{E}={{\vec{E}}_{1}}+{{\vec{E}}_{2}}+{{\vec{E}}_{3}}+. ......+{{\vec{E}}_{n}}$

            (नावेन्दु भौतिकी वर्ग की नोट प्रति के अनुसार अनेक आवेशों के कारण कुल विद्युत क्षेत्र का व्यंजक ज्ञात कीजिए)

प्रश्न(26) - क्या एक उदासीन वस्तु अपने आसपास वैधुत क्षेत्र उत्पन कर सकती है ? उदहारण दे|

उतर:- उदासीन वस्तु अपने आसपास विधुतिय क्षेत्र उत्पन कर सकती है | जैसे - विधुतीय द्विध्रुव 
,समान परिमाण तथा विपरीत प्रकृति के दो आवेशो से बनी हुई निकाय है | जिसके कारण इसका  कुल आवेश शुन्य होता है |फिर भी इसके कारण विधुतिय क्षेत्र उत्पन्न होता है |

प्रश्न(27)- विद्युत द्विध्रुव आघूर्ण का S.I. मात्रक क्या है? बिहार बोर्ड- 2014 , 15 उत्तर - विद्युत द्विध्रुव आघूर्ण = P= q x 2l = आवेश x दूरी = कूलम्ब x मीटर = कूलम्ब-मीटर अतः विद्युत द्विध्रुव आघूर्ण का S.I मात्रक कूलम्ब-मीटर होता है।

प्रश्न(28)-एक समान विधुतीयक्षेत्र में एक विधुत द्विध्रुव रखा हुआ हैं दिखएँ की यह स्थांनान्तरित गति नहीं करेगा ?

उतर:-माना की एक द्रिध्रुव

समरूप विधुतीय क्षेत्र E

मे रखा हुआ हैं |

–q आवेश पर बल

F1 = qE ($\overset{\to }{\mathop E}\,$ के विपरीत दिशा में )

+q आवेश पर बल
F2 = qE ( $\overset{\to }{\mathop E}\,$ के दिशा में )
द्रिध्रुव पर लगने वाला कुल बल
Fnet = F1 – F2= qE – qE = O

अतः द्रिध्रुव स्थांतरित गति नहीं करेगा |

अर्थात् द्रिध्रुव स्थांतरित संतुलन में है |

प्रश्न(29)-विधुतीय द्रिध्रुव के कारण विधुतीय क्षेत्र तीव्रता दुरी बदलने के साथ किस प्रकार बदलती है ?

उत्तर:- किसी विद्युतीय द्विध्रुव के कारण अक्षीय स्थिति में विद्युतीय क्षेत्र की तीव्रता

Eaxial = 2p/4π${{\varepsilon }_{o}}$ r³

Eaxial α 1/r³... (i)

किसी विद्युतीय द्विध्रुव के कारण निरक्षीय स्थिति में विद्युतीय क्षेत्र की तीव्रता

Eequipotential = p/4π${{\varepsilon }_{o}}$r³

Eequipotential α 1/ r³ ... (ii)

समीकरण (i) तथा (ii ) से

E α 1/ r³

किसी द्रिध्रुव के कारण तिव्रता दुरी के घन के व्युत्क्रमानुपाती होता है|

प्रश्न(30)- विधुत क्षेत्र मे वैधुत द्विध्रुव का घूर्णन किधर होता है ?

उत्तर:- विधुतीय क्षेत्र मे विधुतीय द्विध्रुव इस प्रकार घूमेगा कि $\overset{\to }{\mathop{P}}\,$ और $\overset{\to }{\mathop E}\,$ के बीच का छोटा कोण और भी छोटा होता जाएगा।
जब$\overset{\to }{\mathop{P}}\,$ और $\overset{\to }{\mathop E}\,$ के बीच का कोण शून्य हो जायेगा तो यह घूमना बंद कर देगा |

प्रश्न(31) -गुरुत्वाकर्षण बल और विधुत बल मे क्या समानता है ? दोइलेक्ट्रॉनों के लिए इनके अनुपात का क्रम क्या होगा ?

उतर:- गुरुत्वाकर्षण बल और विधुत बल मे बल मे निम्नलिखित समानता है |

(¡) गुरुत्वाकर्षण बल विधुत बल दोनो केंद्रीय बल है |

(¡¡) गुरुत्वाकर्षण बल और विधुत बल दोनो संरक्षी बल है |

(¡¡¡)गुरुत्वाकर्षण बल और विधुत बल दोनो पारस्परिक बल हैं |

(¡v)गुरुत्वाकर्षण और विधुत दोनो बल दुरी के वर्ग का व्युत्क्रमानुपाती होते हैं |

माना कि दो इलेक्ट्रान r दुरी पर है।

Q1 _______ Q2
electron electron

${{Q}_{1}}=1.6\times {{10}^{-19}}C$

${{Q}_{2}}=1.6\times {{10}^{-19}}C$

${{M}_{1}}=9.109\times {{10}^{-31}}kg$

${{M}_{2}}=9.109\times {{10}^{-31}}kg$

${{F}_{e}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\times \frac{{{Q}_{1}}{{Q}_{2}}}{{{r}^{2}}}$.(i)

${{F}_{g}}=G\times \frac{{{M}_{1}}{{M}_{2}}}{{{r}^{2}}}$. (ii)

Apply (i)/(ii)

\[\frac{{{F}_{e}}}{{{F}_{g}}}=\frac{\frac{1}{4\pi {{\varepsilon }_{0}}}\times \frac{{{Q}_{1}}{{Q}_{2}}}{{{r}^{2}}}}{\frac{G{{M}_{1}}{{M}_{2}}}{{{r}^{2}}}}\]

= 0.0416 × 10⁴³

Fe/Fg ~ 10⁴³

अतः विधुत बल और गुरुत्वाकर्षण बल का अनुपात 10⁴³ के क्रम का होता है।

Q.30- आवेश के आयतन घनत्व को परिभाषित करें।

बिहार बोर्ड-2021

उत्तर- प्रति इकाई आयतन के आवेश को आयतन आवेश घनत्व कहते हैं।

आयतन आवेश घनत्व = आवेश/आयतन

$\rho =\frac{Q}{V}$

* आयतन आवेश घनत्व का SI मात्रक $C/{{m}^{3}}$ होता है।

* आयतन आवेश घनत्व एक अदिश राशि है।

Q.31- एक सतह पर विद्युत फ्लक्स को परिभाषित करें।

बिहार बोर्ड - 2019, 2021